|
|
 |
|
| |
|
| | | | | | Aufgabe vom 01.01.2012 bis 29.02.2012 | | | | | | | | |
| | Gesucht ist eine Darstellungsform der Zahl 2012 so, dass nur Ziffern einer Art (und möglichst wenig davon!) vorkommen. Erlaubt sind die Grundrechenarten, Klammern, Potenzieren, Fakultät und Quadratwurzel und man darf sie im Zehnersystem arrangieren. Beispiel:
2012 = 11+1+(1+1)(11-1)^(1+1+1)
Wer unterbietet die Zahl der benötigten Ziffern? Mit welcher Ziffer schafft man die geringste Anzahl?
Ihre Lösungen sammelt Frau Klingenburg ein, erreichbar über klingenburg@mathematik.tu-darmstadt.de. Einsendeschluss ist der 29.02.2012.
Wir losen unter den Gewinnern wieder kleine Preise aus und stellen die Ergebnisse hier zur Verfügung.
Los geht's! | | | | |
| | Folgende Lösungen für eine Darstellung der Zahl 2012 mit möglichst wenig Ziffern einer Art wurden eingereicht, aus dem Lostopf gezogen und erhalten einen Preis:
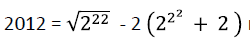 mit nur 8 Zweien (ohne Wurzelexponent) von Thorsten Donges. mit nur 8 Zweien (ohne Wurzelexponent) von Thorsten Donges.
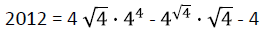 mit nur 8 Vieren mit nur 8 Vieren
von Tim Tanida.
Eine auch sehr schöne Lösung mit 9 Vieren hat Ariel Aronov (5. Klasse) gefunden:
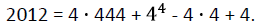
Die Siegerlösung ist jedoch folgende:
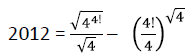 mit nur 6 Vieren von Maksym Berezhnyi. Großartig! mit nur 6 Vieren von Maksym Berezhnyi. Großartig!
Die Mathematik-AG der Edith-Stein-Schule in Darmstadt von Herrn Dr. Reiffert hat sich mit mehreren schönen Lösungen beteiligt und erhält als kleine Anerkennung einen Mathematikkalender 2012 aus dem Mathematikum in Gießen.
Allen Teilnehmenden herzlichen Dank und den Preisträgern eine gute Wahl mit den amazon-Gutscheinen, die diesmal von der AG Didaktik des Fachbereichs Mathematik der TU Darmstadt (Frau Prof. Dr. Regina Bruder) gestiftet wurden.
| | | | | |
| |
|
|
|






