Basic Level Evaluation: The Advertising Pillar
Exercise 1: This is an exercise about an advertising pillar. In point a) and b) you are introduced to two ways of solving the problem. Please carefully try to comprehend those examples!
Exercise 2: Solve part c) and hand it in on the platform.
Problem
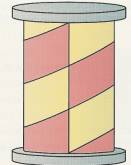 An advertising pillar with a circumference of 4 m and an effectively used surface of 3 m should be completely covered with a glued poster. A two colored composition (like in figure No. 3) should have one line across it, that winds around the pillar exactly 3 times after its glued.
An advertising pillar with a circumference of 4 m and an effectively used surface of 3 m should be completely covered with a glued poster. A two colored composition (like in figure No. 3) should have one line across it, that winds around the pillar exactly 3 times after its glued.
For the draft of the poster with one Plotter, the line shall be defined as shape of a function. The area ration of the two colors shall also be defined by it.
a) Solve the problem, for a line having a consistent slope!
b) What does it look like if the line would show a „rooty“ winding? Use the following function in solving the problem:

c) Why is the following term for a „logarithm“ draft to be preferred,

rather than
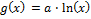 ?
?
Solve the problem by using  .
.
Example of a solution:
a) Consistent Slope 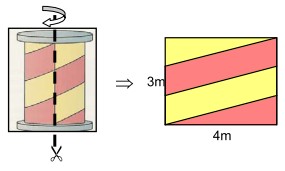
The advertising pillar that is to be covered, can be presumed as a cylinder. Rolled out on one plane, it shows a red-yellow (rot-gelb) hatched rectangle. Because the line is supposed to have a consistent slope that begins down in the left corner and ends in the top right one, it is obvious that the area ration is:
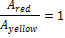
Who ever can not follow that, can also take another approach. This one is used for all the following
subtasks:
The hatched rectangle is put into a coordinate system. Because the line is going around exactly
three times, the rectangle is reproduced two more times and the line extended accordingly.
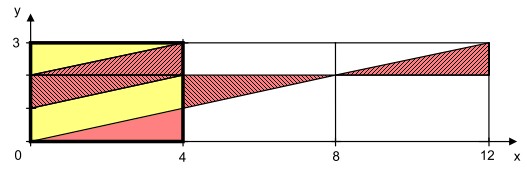
Because the straight line goes through point (0|0) and (12|3), it has a slope of 1/4 and the linear equation is:
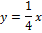
b) Rooty Slope
The function has equation:

To be able to state the area ratio, a has to be defined. Again, like in subtask a), we lay it out in a coordinate system. Because the function goes though the points (0|0) and (12|3), a is taking the value:

So the equation goes:
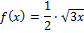
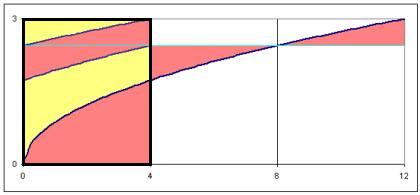
For the calculation of the red area we introduce two possible approaches:
1st
Approach:
If you look at the function:
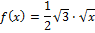
in the interval [0;12], you may calculate the red (rot) area the following way:
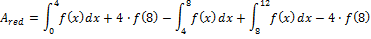
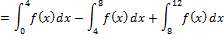
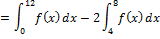
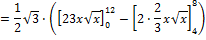
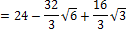
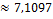
2nd Approach:
Looking at the hatched rectangle in the interval [0;4], you may calculate the red area the following way:
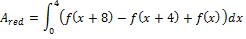

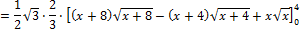
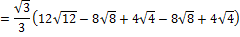
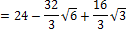
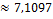
So the area ratio is:

The part of the red area is:
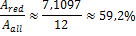
 An advertising pillar with a circumference of 4 m and an effectively used surface of 3 m should be completely covered with a glued poster. A two colored composition (like in figure No. 3) should have one line across it, that winds around the pillar exactly 3 times after its glued.
An advertising pillar with a circumference of 4 m and an effectively used surface of 3 m should be completely covered with a glued poster. A two colored composition (like in figure No. 3) should have one line across it, that winds around the pillar exactly 3 times after its glued.

