Optimization - locker room
In the locker room our trainers give some characteristics of optimization. Choose which offers you want to take.
(back to the math camp)
Technical Presentation
Here is an actual example of different ways of how you can solve a geometric extreme value problem. We are looking at a problem by Heron (100 A.D.) - also called the fire brigade problem
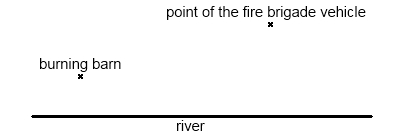
Somewhere in the country side a barn is on fire. The fire brigade responds. They need to fill their tanks with water from the river first. (like shown in the image)
Which point along the river should the fire brigade choose so the whole route would be minimal?
Solution option 1
To find the optimum point P, we mirror point P along the line f to B`. This is appropriate, because the distance BP and B`P are of the same length.
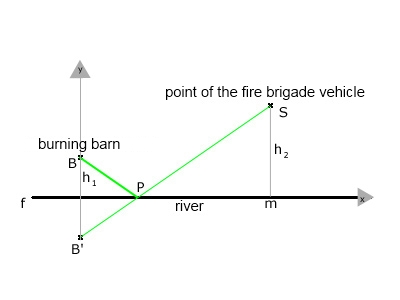
The distance SB`is the shortest distance between S and B`. This we know because of the triangle inequality.
To get the position of the point P, we make the linear equation for the distance SB':
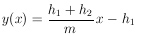
After that we solve the equation for y = 0 and get the optimum value for P:
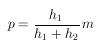
show/ hide
Solution option 2
This option goes by analysis.
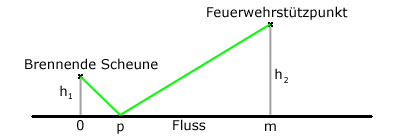
At first we put up an equation for the whole distance S in relation of p:
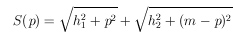
Then we get the first derivative:
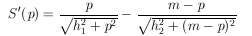
and get for S'(p)=0 after some revision:
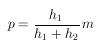
p is a point of extreme of the equation S. If we "wiggle a little on p", we find that p actually is a minimal place of S - our optimum.
show/ hide
Theoretical Lesson
The theoretical lesson introduces a small but important part of basic solution option for (not just) geometrical extreme value problem. TheInfinitesimalkalkül (" f`(x) ... ) as non-basic solution option is not going to be covered here. It should already be known.
In the following paragraph three mathematical tools will be introduced. Their application can be practiced in the fitness room:
The middle inequality
The middle inequality states:
If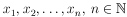 
are positive, real numbers
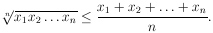
applies. From this it follows that:
"A product of positive real numbers, whose factors have a constant sum, is maximal exactly when the factors are identical." " ([schupp92], page 69)
And on the other hand:
"A sum of positive real numbers, whose terms of the sum have a constant product is minimal exactly when the terms of the sum are identical." ([schupp92], ebd.)
The priciple of niveau lines
The principle of niveau lines is best explained with the help of an example:
"How do you find the minimal distance of a point to a line?"
"Everybody knows the solution. Now, here we look for the geometric place of all points with the same distance from A. They are concentric circles with A as common center. The very one that touches the line g is the solution. It`s radius is the wanted distance." ([CD01])
triangle inequality
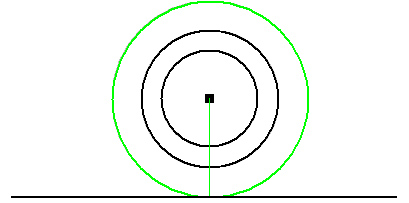
The triangle inequality says:
With complete induction the general triangle inequality goes:
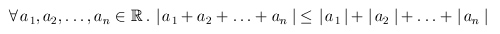
The (general) triangle inequality also applies in every standardized vector space, including R2 and R 3 too.
Background
CAM Software for a milling machine
This is the problem:
There are milling machines, that are able to handle several workpieces at once.
To finish one workpiece a certain sequence of different milling strategies needs to be followed through. Usually that requires different tools. That is why there has to be a change of tools before the next strategy can be milled. If the machine can do several pieces at once we got a optimization problem:
In which order are the single strategies to be done, to mille the different workpieces with as little changes in tools as possible but at the same time mille as many workpieces as possible? As mentioned before, the order in working through the strategies for one single workpiece is set.
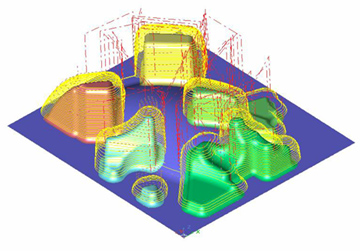
The S.E.S.C.O.I. in Neu-Isenburg has found a solution logarithm already in WorkNC(R)-MPM. Because of legal reasons we cannot go into detail about it`s functionality. MPM was introduced on the EUROMOLD 2002 in Frankfurt am Main.
Further optimizations, that can be done with WorkNC(R) you can find here.
Division of frequencies with GSM-Sending stations
One specific example of soft optimization in economy is the allocation of radio frequencies to sending stations of a mobile phone operator, whose name we cannot mention here, due to a lack of rights. This problem is related to the four color problem:
A mobile phone operator only gets a limited number of radio frequencies within a given span of frequencies for each transmitting station. Otherwise neighboring transmitting frequencies could cut in and interfere.
Neighboring transmission stations are also - because of interference - not allowed to use the same frequencies for transmission of mobile phone calls. In addition to that there must be a single reserved frequency for the transmission of every single mobile call, or there would be interferences.
So how and under which constellations can you assign the optimal frequencies? Is it even possible to do that with the knowledge and the computational power we have today?
From Nature
Let`s look at the optimization processes in nature - especially evolution, as much as it is possible through the glasses of science. These processes are not characterized by goal-directedness for a certain optimum, but by a continual improvement.
The philosophical question, if nature can be presumed as improving itself more and more within given parameters or not will not be clarified here.
The biology example:
The size of bears within different climate zones
Bears in colder regions are usually bigger in volume than bears in warmer regions.
As a reason for that we can assume: The volume compared to the outer layer of the bear, their surface, which is crucial for the amount of heat that is delivered, grows one potency faster.
Das heißt also, dass der Quotient surface/massbecomes smaller (if all bears would have the same density) - meaning less warmth is lost.
Further external links
From math: Extreme value in history
The origin of extreme value considerations can be traced back to the greek mathematicians of old, who included this aspect in their analysis of geometrical constructions. More detailed descriptions for the optimization can be found in Schupp 92. The following example is taken from it. It is the isoperimetrical problem of the plane. In general it states:
"Which of all plane, simply connected areas of same extent has maximum content?" ((Schupp92), page18)
This problem goes back to 900 B.C., when the Phoenician princess Dido requested land for herself and her followers from an African ruler. He allowed her to claim as much land as she can surround with the hide of an oxen. According to the legend Karthago was built on that land.
Vergil (70-19 B.C.) talkes about this event in his Äneis. Justinus (3. century A.C.) mentiones, how Dido had the hide of the oxen cut in stripes to be able to surround a large territory. (read more: (claus92) page 35f)
By cutting the hide in stripes the isoperimetrical problem of plane emerges. It most likely is not a factual report, but the problem still made it into math. The solution of a circle was couched with the development of the differential calculus. Jakob Steiner (1796-1863) seemingly developed an evidence for it with the help of the Steiner`s four-joint-procedure. But all he proved was, if any, the solution should be the circle. Steiner missed to prove the existence of an optimum. To bridge the gulf Karl Weierstrass (1815-1897) (schupp92) or rather by C. Caratheodory and E. Study ((claus92)) brought proof at the end of the 19th beginning of the 20th century.
The isoperimetrical problem of plane, that remained unsolved for over 2000 years, is just one example of extreme value problems, that were shaping the history of math significantly. To read more about it, look at (claus92), for additional examples of historical problems and their solutions.
Optimization in the up-to-date branch of research
Here we are going to look at how optimization methods have and will become part of mathematics. Some of them even became individual branches:
Linear optimization for example, is taught during the first term of math studies in Algebra. In analysis the infinitesimal calculus is worth mentioning, taught in high school. Discrete math shows off with the discrete optimization, applied in todays economy. Not to forget about elementary mathematics or numeric mathematics. While there are only single problems and procedures in elementary mathematics show optimization features, numeric mathematics is a branch dealing only with those problems. Another branch of centrality for optimization is the game theory devoted to different game and winning strategies
Optimization in math lessons
The curriculum of Hesse high schools does not contain "Optimization" as that.
The only place for extreme value problems in high school are in the introduction of infinitesimal calculus as part of the analysis.
For the topic of optimization being brought up during lessons, it is good to incorporate the principle of optimizing as a guideline.
Incorporating optimization as a guideline does not mean to dedicate a whole lesson once in a while to optimization, obviously not included in the Hesse curriculum. It means the more to reveal the thought of optimization within topics, as given.
What could be rewarding about doing so?
From daily life
Our society does not allow us any different, but to plan our daily routines so we waste less resources like time, money, energy or similar things; making the highest profit. Beginning with a new school kid, we plan the optimal shortest, but as a side condition safest, way to school.
Every person following through on various appointments, tries to set the times so no time-gaps in between are useless or wasted. Other daily life experiences like packing a suitcase, wrapping a gift or going for sales at the supermarket are also optimized, otherwise we would not be able to take all our clothing along on vacation, we would have to buy new fancy paper too often or we would not even reach the end of the week with any money.
In sport or even with board games we see the need to optimize motion sequences or game strategies to be better and more successful than fellow campaigners.
We may conclude, that the principle of optimization is essential for our life.
Mathematics offers problems and solution methods to almost every problem introduced, like the shortest-distance-problem, wrapping-problem or as whole branches the discrete optimization and game theory.
An example from the daily life of two students
Two students, Joe and Andy are wanting to combine lunch at the canteen with a visit at the book store. While Joe wants to buy some newspapers Andy just wants to hand in an attendance card for a competition. Joe prefers a stop there after the canteen than before, because he does not want to carry the newspapers along. Whereas Andy does not want to hold the card any longer. They make it their goal to visit the store before lunch. How do the two have to plan their canteen visit so everything gets done in the shortest amount of time, to the satisfaction of both?