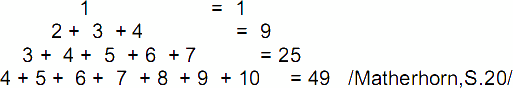Heuristic education
What characterizes naturally good and successful problem solvers? Again
and again there are students who are always quickly coming up with great
ideas to solve a problem. Usually they cannot explain how they came
across this option, they "just had the idea".
Why can't all students just do that? Or, put in other words: How can teachers enable other students to get similar results? An answer to this question
is going to be given here in the theoretical part.
Agility
Good problem solvers show extraordinary agility. This shows especially in
various ways, once they are solving problems by mathematical means:
| Reduction: |
Students reduce the problem intuitively and correctly to the essential basics. |
| Backward chaining: |
Students are good at tracking thoughts. In the right situations this is done automatically. |
| Attention of the aspect: |
They pay attention to several aspects of the problem at the same time, or
recognize the conditionality of things easily and vary them intentionally. |
| Change of aspects: |
They change the assumptions or criteria of any given case to move to
wards a solution. Intuitively various aspects of the problem are looked at, preventing "stagnation". |
| Transfer: |
Smart problem solvers apply a familiar procedure to any other, maybe very
different, context. They usually recognize the "structure" of a problem. |
Usually untrained smart problem solvers cannot utilize these skills consciously. That is why they sometimes cannot explain how they solved the
problem.
As untrained but very good problem solvers are compared to the less agile,
the question arises if there is a link between the uses of strategies in terms
of agility.
The effect principle of heuristic education presents that context precisely:
Lacking agility can be compensated partly by learning and applying heuristic procedures and techniques intentionally, which lead up to achieving
similar results of those great, agile minds with their subconscious thoughtprocesses.
Heuristic procedures
From here on it can be learned which basic heuristic procedures there are
and how they can make up to compensate a lacking in agility.
Heuristic Means
|
Heuristic strategies
|
Special heuristic principles
|
General heuristic principles
|
| |
|
|
show all |
Informative figure
If students have learned that the measure of a value can be visualized by a
certain length of a distance, intelligent solutions of agile students are easily
understood by others too. More basics:
amount, size, parts |
visualized by length |

|
|
by square |

|
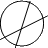
|
by a circle |
|
Product of two numbers
a · b |
area of a rectangle |

|
Product of three numbers
a · b · c |
volume of a cuboid |

|
Association of two values
|
chart of values |

|
|
coordinate system |

|
|
equation, term |
|
Seats - on - a - bus - problem
One third of seats on a bus are taken by kids. 6 seats more are taken by
adults. 9 seats are remaining empty. How many seats are on the bus?
Solution by informative figure:
This means one third is 15 seats. Which means a total of 45 seats.
Graphic solving
Impressive examples are available for graphic solutions of equations and inequality:
A timber yard stores 135 square meters of birch wood and 114 square meter of spruce wood. Daily 7.5 square meters of birch wood and 6.5 square
meters of spruce wood are removed. After how many days will the
amounts of both kinds of wood be equivalent?
Even though the issue is not very practical, it helps gaining many interesting insights.
People solving this problem by means of equation, are missing out on the
fact that at the calculated point of time none of the wood of one sort is
even left!
Graphically presented, you would recognize how the x-axis of the wanted
intersection is greater than the zero point of one of the two linear functions
of the interpreted shipping procedures.
A thorough discussion and consideration of these problems may generate
far more mathematical insight and applicational skills than the strict (formal) solving of 10 others!
Generalization:
Working with geometrical illustrations often leads to a deeper understanding of mathematical contexts too.
Example:
Solving quadratic equations can be considered for example, as an intersection of a parabola and a straight line: x2- 2x +8 =0 equals x2= 2x -8. Hereby the different possibilities for the existence of solutions of quadratic
equations can be highlighted, instead of just a sole algebraic approach.
Strategy of forward chaining
Possible introduction via brick-wall-problem or mathematically related:
Geometry
The measures of a body are given (cuboid, prism, ...). List all the things
that can be calculated from it!
Or further: What can be done with this? (Even constructing and developed
views would be part of this...)
Algebra
An equation is given, i.e. x - 7 = 9
How can the equation be made more difficult?
(numeric value, putting
brackets, introducing factors, quadrate it,... )
What are equations for?
(formulas, describing contexts,...)
Typical questions for forward chaining:
What is given?
What do I know about the information given?
What can I identify as a result of it?
Strategy of backward chaining
typical problems are:
Apple problem
A man goes and picks apples. He has to pass 7 gates to get back into town.
At each gate a guard claims half of his apples plus one. In the end all that
is left for the man is one apple. How many did he have in the beginning?
Dice-making-problem
Two dice of different sizes are knead together (edge length a1 and a2) for
one. How big is the new surface of the dice?
Problem variation
The two dice are supposed to make up a cuboid with only integer edge
lengths. How many different possibilities are there?
Systematical testing
Purposefully searching for regularities or values by looking at special
cases from a classifying point of view.
(i.e. vertical throwing, packing
boxes; for example, in coming across extreme value problems)
Profile for systematic testing
Invariance principle
Sewerin writes: "Some processes have characteristics, that are invariant to
changes. Especially with mathematical tasks of coloration, plastering,
chess patterns or graphs, just as with games, you get really close to a solution by looking for invariant characteristics." Sewerin, H.: Mathematische Schülerwettbewerbe.- München 1979, page
141.
The invariance principle supports the strategy of systematical trying in
particular. The invariance principle in a broader sense means a search for
constants, reference values or similarities in the information of the problem posted.
One of the first subconscious interactions with the principle of invariance
is usually a general situation with a broad diversity of options to choose
from. Someone may not know where to begin narrowing down the field of
options. A typical example is a puzzle, where the idea to start with selecting all boarder pieces to frame the picture, comes to mind pretty fast.
Additional experiences may be gained by special riddles like cryptograms and magical triangles or squares. An important similarity of such riddles
lies in picking the correct option of many possible proofs, which abides by
the given requirements.
Among the cryptograms, certain key numbers like 1 and 0 play an important role as invariances. 1 is borrowed, if a digit number of a sum out of
two terms of a sum is bigger than the number of each addend up.
Sewerin schreibt:"Manche Prozesse besitzen Eigenschaften, die bei Veränderungen
invariant bleiben. Besonders in mathematischen Aufgaben über Färbungen,
Pflasterungen, Schachbrettmuster oder Graphen sowie bei Spielen kommt man der
Lösung sehr nahe, wenn man solche invarianten Eigenschaften sucht."
Sewerin, H.: Mathematische Schülerwettbewerbe.- München 1979, S. 141.
Example: The letters are to be replaced by digits - same letters meaning
same digits and different letters meaning different digits.
S E N D
+ M O R E
-----------
= M O N E Y |
O N E
T W O
T W O
T H R E E
+ T H R E E
--------------
= E L E V E N |
Links to previous experiences may develop, as challenging situations arise
during math class (problems - in a broader sense) that have an analog heuristic background. Usually such problems are not very praxis related, but
contribute drastically to the ability to think. Limiting the options of
choice in decision situations is an intelligent accomplishment, closely related to reality: deciding for a new piece of cloth, a more favorable insurance etc. In such situations it proves useful to be aware of the subjectively
different invariances like: use of the item, personal taste and wallet etc. to
prevent a later regret of the decision made. It is worth a try to let students
discover similarities in the approach of mathematical problems and practical decisions of choice. This is more motivating than the solving 10 new
sample problems!
Such examples are about specific invariant characteristics, features, relations or values. In "Matherhorn", where the above problem is taken
from, certain problems may be found to practice the recognition of invariances, like looking for patterns in the following term structure.
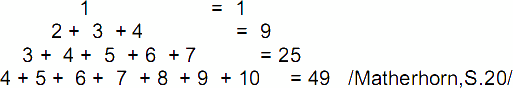
The finding of rules for the creation of number sequences, supplementing groups of figures according to an outline first recognized - a popular
part of IQ tests - can easily be interpreted as good applications of the principle of invariance. If it is not possible to quickly find a solution, it also
proved helpful to give a hint like: "Search for similarities or common
points of relation." to keep students from aimless wondering thoughts,
and leads up to a more goal-oriented analyzation of the problem situation.
This does not give a guarantee for a solution, but limits the scope of search
immensely, and by that increases the chances of success. Heuristic education has been successful if the students are able to generalize their experiences of problem solving, like expressed in the hint given above.
Further applications:
- Motion problems (constant speed differences)
- Age problems (age difference of two people is always the same)
- Miscellaneous problems, Addition problems ...: Invariances can
be constructed, when two processes are made comparable by their relation to what happens within a certain time unit.
- Last but not least: The percentage calculation and the rule of three as
samples of the work with invariances.
Principle of case differentiation
Search for a complete partition of the complex assumption, or the original
relation of the statement of the problem in a series of simple accessible assumptions or relations.
Extremum principle
Search for sets that meet the marginal conditions of the statement of the
problem or rather for extreme cases of all possible ones.
Example
At the end of the day a tire service for motorbikes and cars determines that
all the tires of 24 vehicles have been changed (without the spare tires). The
total amounts to 68 tires. What is the total of motorbikes and cars (excepting the spare tires) that have gotten new tires?
Of course this problem can be solved properly by solving the system of
equation.
But you can also argue "context-wise", how at least two tires per vehicle
have been changed, which would make 48 tires, if it were only motorbikes.
The difference in tires makes 20, that could only be changed on cars. So it
would have been 10 cars and 14 motorbikes for the day. There is a very
important heuristic principle concealed in this argument: the extremum
principle - see also the examples for the invariance principle.
Symmetry principle
Looking for symmetries (identical analogies) among the elements of the
problems given quantity of information.
Example
Proof that for all positive a,b,c the following applies:
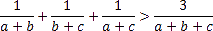
If the less agile or heuristically untrained student does not recognize the
symmetry of the term structure of this inequality, he will come up with any
knowledge possibly applicable. Most of them will remember how it is
necessary and helpful with some fraction equations to get rid of the denominator. A schematic approach would be to form a common denominator as a product of many denominators. This is going to prove very ineffectual. Now having awareness proves useful when proceeding, in case a
commonly sound idea proves inappropriate.
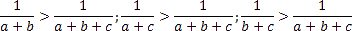
With this, another particularly appealing idea to prove something is found.
Agile students will strike on this idea automatically; or heuristic educated
students by more or less conscious alignment to heuristic procedures:
in this case the partition principle or symmetry principle.
Partition principle
Searching for known elements among the entire information of the statement of the problem, by segmenting, and if necessary accentuated new assemblage of the amount of information given (restructuring).
Lernumgebung zum Zerlegungs- & Ergänzungsprinzip
Working on individual and special cases
Choosing individual cases for clarification of a problem or special cases
for sake of assessing part solutions and inspirations for the solution of the
entire problem.
Principle of analogy
The updating and structuring of already gained experiences in problem
solving in regard to the possibility of drawing analogy conclusions.
Such a conclusion drawn from analogy exists if a similarity or likeness to
the statement of the problem as a whole, or its components implies. As
components relate to an already solved problem, they might allow implications on how to proceed in solving the problem at hand.
Heuristic means are useful to support the application of the principle of
analogy.
Principle of reversion
Restructuring, extending or eliminating information from a problem with
the objective of drawing analog conclusions.
Special heuristic principles serve to support or imply a reduction to the in
formation known.
Check-questions:
- What is meant by problem solving?
- Which are the objectives of learning how to solve problems in math
class?
- Which expectations have to be raised to foster a proper learning environment or creativity?
- Which expectations result from this for teacher and students?
- What are thinking skills? How does agility become apparent?
- Heuristic education is central for learning how to solve problems.
What is meant by this?
- What is the "operating principle of heuristic education"?
- What heuristic strategies and methods are there?
- What needs to be considered, if heuristic procedures are going to be
made part of lessons?
- What is the difference between heuristic and other mathematical (algorithm and calculus) procedures?