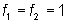Fibonacci numbers

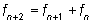Fibonacci numbers (f1, f2, f3, ...) go back to the question about the increase of rabbits, published in 1202 by Leonardo of Pisa (known as Fibonacci) in his arithmetic book Liber Abaci.[1] The solution is, that at the end of n month the number of pairs of rabbits is fn with

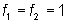and .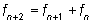

In addition to this recurrence formula there is an explicit formula too for the Fibonacci numbers[2]

n

1

2

3

4

5

6

7

8

9

10

11

12

fn

1

1

2

3

5

8

13

21

34

55

89

144

By this recurrence formula, EXCEL can relatively quickly create the first 100 Fibonacci numbers, as f1 and f2 are given and f3 is assessed as

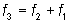
and this regulation of generation is copied analog for f4 to f100.

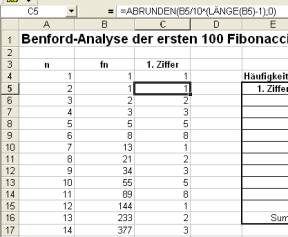
Assessment of initial digit frequency in EXCEL

1. First digits assessment

To assess the first digit distribution it helps to separate the numbers examined into first digits and to write it in separate slots:

by EXCEL command:

=ROUND(B5/10^(LENGTH(B5)-1);0)

you get, for example, the first digit of the number in cell B5.

2. Assessment of the frequencies of the single first digits

If the first digits are noted separately in a column (like column C), it has to be counted how often the single digits are in this column. This can be done with the EXCEL feature "COUNT IF", which counts all non-empty cells of a section and its contents that are conform to the research criteria.

The absolute frequency of the first digit 3 in column C is incidental from the formula

=COUNT IF(C:C;3)

[1]See Dudley (1999), Page 272.

[2]Please note that the explicit formula of Fibonacci numbers includes the golden ratio

For large n by approximation one has

whereby you can show, that the quotient of successive Fibonacci numbers for n → ∞ strives to the golden ratio.