How can teachers help their students learn to solve problems effectively?How can teachers help their students learn to solve problems effectively?Objective: to gain an overview about various heuristic methods to support learning how to solve problems.
Imagine you have misplaced your key. You could either panic and get help to open the door or calmly search for it. If you carefully think about the last time you saw the key somewhere, you can reconstruct those experiences in your mind and identify where you left it.
Whoever proceeds like that uses an important problem solving strategy: backward chaining
You ask yourself:
A substantial amount of information can be learned from this common problem:
Impressum: Bruder, R.: Kreativ sein wollen, dürfen und können! In: ml Heft 108
Bruder, R.: Lernen, geeignete Fragen zu stellen. Heuristik im Mathematikunterricht. In: Mathematik lehren 115 (2002), page 4 - 8
List class room conditions that create a positive learning environment which will allow students to master difficult tasks!
Problem solving strategies are also referred to as heuristic strategies. They cannot guarantee solutions but are often invaluable in solving problems.
Have you heard of these strategies?
What other strategies do you know? How did you come across those
strategies?
Your existing problem solving strategy is only employed when you cannot solve a problem right away. Look over the problems listed below. Identify one for which you need to think and develop a strategy. Focus on the process you use to develop the strategy in your mind and write it down for yourself!
Let us use your existing strategy for solving problems on the following tasks!
As you look over the tasks:
What are the questions you ask yourself?
How do you proceed when you encounter a challenging mathematical
problem?
Use one of the examples below to describe your current problem solving
model!
Usually you are trying to remember similar problems (principle of analogy) or associate certain mathematical procedures according to terms, mentioned in the task. Or you try tracing the unusual situation back to a familiar one (principle of tracing back).
Maybe you have put the first task aside, because you thought of mastering it simply by complete induction.
You think to yourself: Sure, that works, boring (everything is relative!) and not necessarily called neat. But heuristic strategies help in finding neat solution options too!
Let us stick to the first problem. A nice option of solving this problem presents itself if the symmetry principle is applied here in a sense of creating"missing" symmetries in a broad understanding of "harmony" and "fitting":
What is annoying here, is the 11. If there was a 12 instead, something useful may be concluded for the division by 6. So let`s just create a 12!
The term looks solvable like that:
n3 + 12n - n
Now it only needs to be examined that the expression n3 - n can be divided by 6. The division principle helps us here forwards and backwards:
forwards: n3-n = n (n2-1) = n ( n+1) (n-1) a product of three successive natural numbers!
backwards: division by 6 demands a possible division by 2 and 3.
Because the product of three successive natural numbers can always be divided by 2 and by 3, we have proven the liability of the statement 6/n3+11n for all natural numbers n>0.
This is most likely what you dealt with in "age problem" no. 3 too. A little further down the road of Secondary Level I, something like that could be solved by means of equations. But what can be done, if students do not know about this resource yet?
Something like an informative figure may be of help here, for the distances of the age differences can be marked. It also works with EXCEL. Try it yourself!
In problem 4 the informative figure can be even more convincing - depending on your own preferences for various options of problem solving.
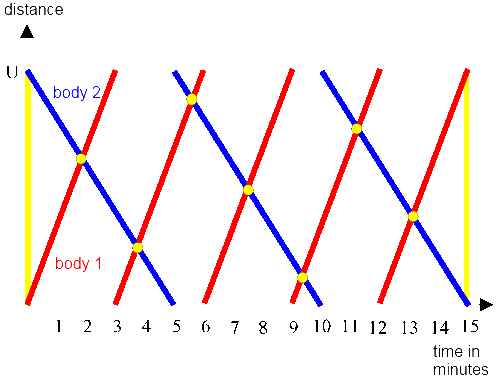
It can be read off the figure, that the two bodies meet 8 times within 15 minutes. The meetings always happen at the same interval, they pass every 15/8min, which is 112,5 sec.
The meeting points part the circle in 8 equal sections. The faster body passes 5/8 of the circle, the slower one 3/8.
There are several solutions for the Trabbi problem. The difficulty is in the confusing way the question is articulated. By introducing variables and introducing equations the confusion may disappear. A graphic interpretation is also very useful. Informative figures, variables/ equations are heuristic means.
Also very interesting is the ball problem. This problem was set for the day of mathematics (class 12). There are different approaches, leading to one solution: you try finding the invariances by reduction: The ball pyramid can be reduced to a tetrahedron of ball epicenters or a cube surrounding the ball pyramid.
Problem 7 has already been part of the initial self test. It is an example of a certain heuristic principle, the transformation principle. In addition to healthy (heuristic) understanding, some detailed mathematical knowledge is required i.e. about the position of the orthocenter of an equilateral triangle, Pythagorean theorem,...
Unfortunately this often leads to these more challenging problems being dropped, because students are not familiar with all required "basics", or they ask, if this problem is going to be part of the test. If it is not part of the upcoming test, it is not considered important.
Heuristic strategies can only be acquired by experience, if not already intuitively known.
Költzsch (1979) gives methodic rules, describing an heuristic learning method:
The context in which a strategy is learned, proved to be very important too. These strategies are not randomly transferable. You have to think carefully of the examples used, to develop a new strategy. The strategy will be intertwined with the context that has been introduced with it.
This may also be an advantage, if the introduction problem gets a figurative name - which can intentionally be used as a link, to enable you to remember certain procedures in different contexts and support a transfer.
Unfortunately this often leads to these more challenging problems being dropped, because students are not familiar with all the required "basics". Or they ask if this problem will be part of the test; if it is not part of the upcoming test, it is not considered important.
What opportunities in designing lessons do you see to address the problem described? The problem being: students are so rarely confronted with more difficult problems.
