Benford`s Law - Plausibility considerations

Start | Overview of problems | Literatur | Credits 

Plausibility considerations

Besides the formal plausibility considerations based on the scale invariance, there are several ways and reflections to trace Benford`s Law intui tively in a plausible way. Especially in class it may help to get results on a more intuitive way by making plausibility considerationPage

This paper introduces more useful mathematical considerations to help make Benford`s Law more plausible by intuitively revealing deeper mathematical elementPage

Plausibility considerations by Humenberger (Tunnel)

Problem: Tunnel (**)

The ventilation system of a tunnel turns on and off automatically. During each full hour it operates for 35 minutePage Turned on at 11:00 a.m. it will turn off at 11:35 a.m.. It is of no importance if it is turned on at the top of the hour or any other point in time.[5]

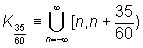
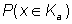  1. What is the probability a car will drive through anytime while the ventilation system is operating?
  2. What is the probability for a random moment in hours (i.e. a randomly picked real number) to be a part of the indefinite set

    ?
  3. Assess in general for 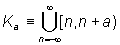with 0 <a ≤ 1!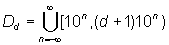
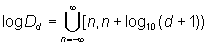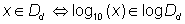    Now those considerations are to be linked to the Benford Law. Therefore we point out that the amount of all positive, real numbers with the first digit ≤ d can be denoted as

    with d = 1, ..., 9.
    By taking the logarithms of the set Dd the outcome is:
    ,
    for which
    applies.
  4. Assess the probability
    .
  5. Conclude the probability

    and

    Interpret your solution!

Problem: Integration (**)

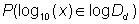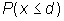
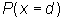
Come up with another possible imbedding for the above problem!

 

(chapter overview)

Reduced random variable according to Krämer

For this plausibility consideration, we go back to the common result of constant random variables modulo 1, which are called ‘reduced random variables’, effectively representing the decimal places of the original random variable. For example, for the random variable X having the value 4.82 , X modulo 1 has the value 0.82. The point is, that the decimal places for many constant random variables have a wide domain with mostlyequal distribution.

Since it is very hard to prove this during an academic lesson, Krämer suggests a plausibility consideration with the example of a wheel of fortune. If the wheel is turned on hard enough, it becomes intuitively clear that each sequence of the wheel has the same probability to win. Imagine a wheel with extent 1 and the random variable X representing the total distance from the original apex, so the reduced random variable °X is the distance of the original apex to the zenith. °X can only take on values from 0 to 1. It soon becomes clear how - with an increase of the range of X, meaning more turns of the wheel of fortune - the reduced random variable °X increases between the interval [0,1].

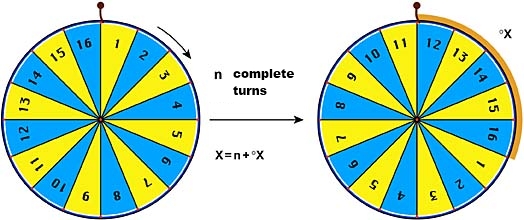
These considerations now to be linked to the Benford Law. The first digit of a randomly chosen number X is exactly the digit k, if a suitable n abides by:

.

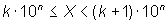By drawing on and applying laws of logarithm, we get the equivalent equation:

Because k can only take the value between 1 and 9, and n being a natural number, one may conclude that the equation is fulfilled when the decimal places of log10(X) are between log10(k)  and log10(k+1). If the random variable log10(X)is denoted as Z and the decimal places as °Z,the above equations are equivalent to:

.

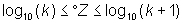As reduced random variables (meaning the decimal places) of Z=log10(X), °Z only takes on values between 0 and 1. Considering the above wheel of fortune model, we may also conclude that °Z is almost equally distributed, and that is why the probability for it to be part of one certain interval section, is proportional to the length of the interval. This assesses the probability

,

which is the same as the probability given by Benford for k as the first digit.

 

(chapter overview)

Choosing a number from the first n natural numbers

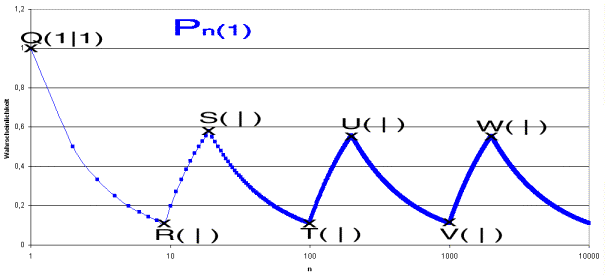
Imagine a game where you are to choose any natural number from 1 to infinite. How likely is it that your number will have the first digit 1? If the choice should be a natural number between 1 and 13, we would be able to answer quickly. On the supposition that all numbers are equiprobable, the probability is 5/13, because in this interval 5 numbers (1,10,11,12 and 13) begin with 1 as initial digit.

Now the game is to be simulated for the choice of a number from the first natural numbers n, so that we get the probabilities Pn(1) for the first digit 1 as subject to n. These probabilities Pn(1) can also be visualized as the drawing of a number from an urn, that contains n of the first natural numberPage If n=1, there is no other number in the jar, so that P1(1)=1. For n=2 the numbers 1 and 2 are in the urn and P2(1)=1/2, for n=3 is P3(1)=1/3, etc.

Problem: Initial digit 1 (***)

  1. Assess the probability of Pn(1) as subject to n. Complete the following chart up to at least n=30!
    n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 ..
    1                                            
  2. What sort of n increase or decrease Pn(1)? Which n is Pn(1) minimal, which n for is Pn(1) maximal? Consider all n up to 1999!
  3. The figure shows the mapping of Pn(1) on top of n. What are the coordinates (n|Pn(1)) of the marked points R ľ W? Please note that the
    abscissa is divided in logarithms!
  4. The probability P(1) for the first digit 1 fluctuates between a constant minimum U(1) and an almost stable maximum limit. The sequence of the maximum limit

    is to be examined closer. Define the limit of sequence of Om(1) for m → ∞! 
    (Please note: Find a closed term with
    )
    The numerator is

    with m representing the set of places from 11 ... 1. The denominator can also be denoted as
  5. Which conclusions can be drawn from the probability P(1) of the first digit being 1, based on the considerations above?

Problem: First digit 9 (**)

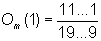
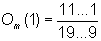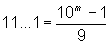
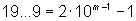
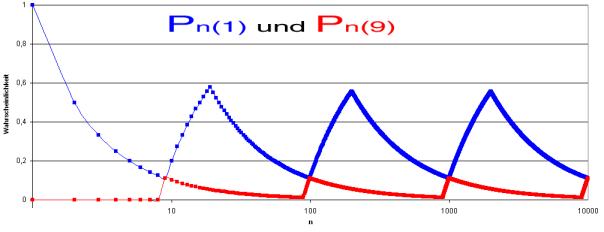
Now we consider the probabilities of Pn(9), the probability of any ran domly chosen number from the first natural numbers, begins with a 9. In the figure are the courses of both Pn(1) and Pn(9).

  1. Which n have Pn(1)=Pn(9)?
  2. What is the range of the limits of Pn(9)?
  3. What conclusions can be drawn from the considerations above about the probability P(9) of the initial digit 9 to occur?

Problem: All first digits (**)

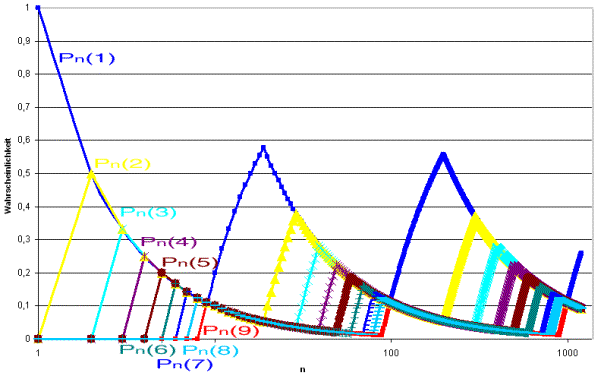
Even for all other initial digits k from 2 to 8, the probabilities Pn(k) can be assessed. In the figure below the probabilities of all first digits are given as continual equationPage

  1. What sort of n are all first digits equiprobable?
  2. What do you think about the following statement:
    „The digit 1 is preferred over a long period of time with every newly added place, before the other digits one after the other are catching up on this backlog.” [6]

 

(chapter overview)

Geometric series and exponential growth

The following statements rely on the geometric series or the exponential growth of the values examined, [7]where the Benford Law is intuitively incidental. (Geometric series and the exponential growth are closely related. One is the equalization or the discretization of the other.) Looking at a common sequence of numbers, the number 1 is not further away from 2 than a 5 is from 6[8], But if it is about values that are conditioned to time, the distance between 1 and 2 can be much longer than the distance from 5 to 6. This can be demonstrated with the german share index (Dax) and deepened with the help of a problem (either about the increase of funds or radioactive decay).

Example: German share index (Dax)

Assume the german share index is at 1,000 points, the leading digit is 1. To get an index with the first digit 2, the average index would have to double,
which indicates a growth of 100%. If the Dax is at 5,000 point already, only a 20% increase is needed to get to the new first digit 6. Finally, having a Dax of 9,000 points, only requires an increase of about 11% to have the 1 supersede the initial 9. The 1 again stays at the beginning until the index has doubled, this time from 10,000 points to 20,000.[9]

Choose one of the two following problems, to study more in depth:

increase of funds or radioactive decay.

Problem: Increase of Funds[10] (**)

A fund of K(t0=0)=10,000€ is deposited at a 7% interest rate. Consider the development of the funds annual interests, including compound interest.

  1. Show that the following term applies, for the time t1 (in years), the increase of funds K from 10,000€ to 20,000€ takes:
  2. How long does it take for your funds to increase from:
    1. von 20.000 € to 30.000 €,
    2. von 30.000 € to 40.000 €,
    3. von 40.000 € to 50.000 €,
    4. von 50.000 € to 60.000 €,
    5. von 60.000 € to 70.000 €,
    6. von 70.000 € to 80.000 €,
    7. von 80.000 € to 90.000 € and
    8. von 90.000 € to 100.000 €?

    Please use a chart!
  3. Give an equation that assigns to every first digit d the time td that the funds K take to increase from the first digit d to the first digit (d+1)!
  4. How does a different rate of interest effect the equation?
  5. Show this context with the help of Benford's Law!
  6. Is it plausible to believe someone who said, “over the next 34 years, 1 will occur as a first digit as often as the first digit 9 in the funds”?

Problem: Decay (**) 

The decay of radioactive compounds is denoted by law as:

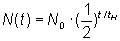
with N(t) referring to the number of nuclei not under decay at the time t, and N0 the number of nuclei at the time t=0. The half life tH is the time
necessary for half the original nuclei to decay.

The radioactive compounds Polonium 210 decays with a half life of 138 dayPage Assuming a starting time of t=0 with 100,000 nuclei, assess, by means of the given equation, the times that the first digit of the set of nuclei changePage

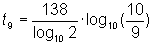  1. Show that for the period t9 (in days), where there are between 100,000 and 90,000 Polonium nuclei
    is applicable!
  2. How long will there be...
    1. ... between 90.000 and 80.000 nuclei?
    2. ... between 80.000 and 70.000 nuclei?
    3. ... between 70.000 and 60.000 nuclei?
    4. ... between 60.000 and 50.000 nuclei?
    5. ... between 50.000 and 40.000 nuclei?
    6. ... between 40.000 and 30.000 nuclei?
    7. ... between 30.000 and 20.000 nuclei?
    8. ... between 20.000 and 10.000 nuclei?

    Please use a chart!
  3. Give an equation that links the first digit d to time td, the number of radioactive nuclei begins with a first digit d!
  4. What effect would another half life have on the equation?
  5. Illustrate the context with the Benford Law! 

 

(chapter overview)

Remark

The considerations above show that the initial digits of numbers of geometric series or exponential growth abide by Benford`s Law. It is not possible to prove mathematically why nature does not count in arithmetic series (1, 2, 3, ...) but in geometric series, which leads to uniform distribution. Benford acknowledged this context as a kind of natural law that lacked empirical proof.[11]

Other than the considerations above, do nothing to consider why other values, mainly those that do not change over time, abide by Benford`s Law too. A typical example of such values is the magnitudes of bodies of water. No matter what units are used to measure, the result will always prove Benford`s probabilitiePage With a look at the composition of the world, the following is made clear: Because there are more puddles than ponds, more ponds than lakes, and more lakes than oceans, there will be obviously more waters between 10 ha and 20 ha, than between 20 and 30 ha and more waters between 100 ha and 200 ha than between 200 ha and 300 ha.[12]This matter aside, the scale invariance also provides an explanation as to why dimensional sizes abide by Benford`s Law. For the house numbers of the american scientists (compare Benford`s diligent work), neither the scale invariance nor the considerations of geometrical series and the exponential growth can be relevant. A plausibility consideration is given in the choosing of a random number n from the first natural numbers.

 

(chapter overview)

[1] See Humenberger (2000), Page 146-147.

[2] See Krämer (1990), Page 49-52 und Krämer (2005), Page 68-70.

[3] See Flehinger (1966), Page 1056-1061, Raimi (1969b), Page 112-113, Humenberger (1997), Page 42-48 and Humenberger (2000), Page 139-143.

[4] See Dworschak (1998), Page 229 and Hammer (2001), Page 428-429.

[5]In this example it does not matter if the ventilation was turned on for 35 minutes at the top of the hour or any other fixed point in time.

[6] See Humenberger (2000), Page 140 and Humenberger (1997), Page 43.

[7]The geometric series and the exponential growth are directly related. One is the smoothing or discretization of the other.

[8] See Dworschak (1998), Page 229.

[9] See Dworschak (1998), Page 229.

[10] See Hammer (2001), Page 428-429.

[11] See Humenberger (2000), Page 144 and Benford (1938), Page 562.

[12] Dworschak (1998), Page 229