Benford Law - Scale invarianceBenford Law - Scale invarianceStart | Overview of problems | Literatur | Credits
The scale invariance is a basic feature of the invariance of Benford`s Law. According to it, any set of data can be multiplied by positive real numbers, that do not change the first digitsdistribution. Reason for this is, that for a universal law of the distribution of digits, the units data are stated in should not matter, because units are not natural but mostly human made. It should not make a difference for Benford`s Law, if prices are stated in euro, dollar or francs. The individual digits would vary because of their conversion into another currency, but the all in all distribution, i.e. the fact that one third of the numbers begin with a 1, should apply after the exchange just like it was before.
If something like a universal distribution of naturally occurring numbers exists, i.e. with the areas of lakes, it should apply independent of any unit created. Even if there would be inhabitants on Planet Zob measuring their areas in Zinkolis[1], they would notice the same distribution as we do, measuring in square meter and are.
In 1961Pinkham was able to proof the scale invariance of the probability distribution given by Benford. On top of that he was able to proof, that Benford`s Law was the only possible distribution that fulfills its condition. If there is a scale invariant distribution, it must be the Benford distribution.[2]
Presented are:
The following proof presented here, was brought in 1976 by Daniel Cohen. [3]Cohen deduced the Benford`s Law as discrete distribution from
the scale invariance Roger Pinkham required in 1961.
The scale invarianceis to be evaluated on sets of data multiplied with factor 2, thereby giving the probabilities of the leading digits being 1. In the second part the set of data is to be multiplied by factor 3, to show the probabilities of the digit 2. The derivations of the probabilities of the other digits are analog.
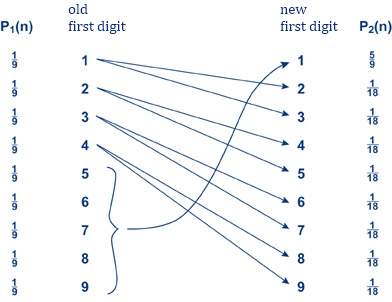
The following chart shows, that numbers starting 5, 6, 7, 8, and 9, after doubling have a 1 as leading digit. After doubling numbers with a leading 1, either a 2 or a 3 will show in the beginning. Halfway through the first digits 2, 3, and 4 become the new leading digits "4 and 5", "6 and 7" and "8 and 9". Furthermore the figure also states probabilities, that show how the condition for scale invariance incompatible to the uniform distribution. Whereas the first digits on the left side are all occurring equally frequent, the right side shows an obvious shift towards the first digit 1 after the doubling, which contradicts the scale invariance, according to which P1(n) = P2(n) should apply, in reference to the labels in the figure. The short notation P1(n) stands for the probability, of the first digit of a number prior to a doubling is n and P2(n) stands for the probability of thefirst digit of a number after the doubling being n.
Instead of the known probabilities from uniform distribution of 1/9 the
more general probabilities of P(1), P(2), P(3) etc. are to be used. Because
of the scale invariance`s condition of P1(n) = P2(n) there is no more disinction made between the first digits before and after doubling. From now
on P(n) will only be used.
According to the following chart there are relations between the particular
probabilities, generally stated as: P(n)=P(2n)+P(2n+1) Furthermore thefirst digits were continued, whereas the two place digits represent the first
two leading digits. P(n) is the short notation for the probability, that the first two digits of a number are the same as the digits of the two place digit n.
The top equation P(1)=P(5)+P(6)+ P(7)+P(8)+P(9) is of no more importance here. Instead we start with the second equation P(1)=P(2)+P(3) and
insert more and more of the equations below. The following equations can
be stated for P(1):
P(1)=P(2)+P(3)
P(1)=P(4)+P(5)+ P(6)+P(7)
P(1)=P(8)+P(9)+ P(10)+P(11)+ P(12)+ P(13)+P(14)+ P(15)
P(1)=P(16)+P(17)+P(18)+P(19)+...+P(30)+P(31)
...
P(1)=P(2k)+P(2k+1)+ …+P(2k+1-1)
The sum of these k equations is:
.
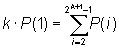addition of P(1) on both sides results in
.
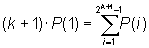If m=k+1 is substituted the outcome is
. (*)
Because every number must start with a digit from 1 to 9, the probability of P(n) applies:
P(1)+P(2)+P(3)+ P(4)+P(5)+P(6)+ P(7)+P(8)+P(9)=1,
On top of this
P(10)+ P(11)+P(12)+...+P(98)+P(99)=1 and
P(100)+P(101)+P(102)+...+P(998)+P(999)=1 and
P(1000)+P(1001)+P(1002)+...+P(9998)+P(9999)=1 and so on.
If the equations from above are added up, the result is:
P(1)+P(2)+P(3)+P(4)+P(5)+P(6)+P(7)+P(8)+P(9)=1
P(1)+ P(2)+...+P(98)+P(99)=2
P(1)+ P(2)+...+P(998)+P(999)=3
P(1)+ P(2)+...+P(9998)+P(9999)=4
...
P(1)+ P(2)+...+P(10k-2)+P(10k-1)=k
Because k=log10(10k) the following average satisfying approximation is apparent with the help of the equation derived from scale invariance (*):
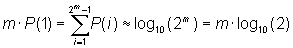
Divided by m we get the probability we were looking for the appearance of 1 as initial digit:
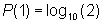
Hereafter the set of values is multiplied by factor 3 to derive the probability of the initial digit 2.
The probability of the occurrence of the first digit 2 is to be derived from the following chart, showing the scale invariance with the multiplication of the original data by factor 3.
We begin with the sum of both equations from above (P(1)=P(3)+P(4)+P(5) und P(2)=P(6)+P(7)+P(8)) and insert more and more of the equations below. The following equations can be stated for P(1)+P(2):
P(1)+P(2)= P(3)+P(4)+P(5)+ P(6)+P(7)+P(8)
P(1)+P(2)= P(9)+P(10)+P(11)+...+P(24)+P(25)+P(26)
P(1)+P(2)= P(27)+P(28)+P(29)+...+P(78)+P(79)+P(80)
P(1)+P(2)= P(81)+P(82)+P(83)+...+P(240)+P(241)+P(242)
...
P(1)+P(2)= P(3k)+P(3k+1)+P(3k+2)+…+P(3k+1-2)+P(3k+1-1)
The sum of these equations is
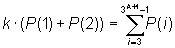
addition of P(1)+P(2) and substitution of m=k+1 we get
,
From this come the average satisfying approximation is:
.
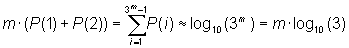Divided by m and the result from above in place of P(1), we get the probability we were looking for the appearance of 2 as initial digit.
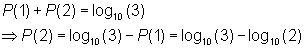
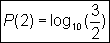
We do not deduce the probabilities of the other first digits here, because it follows the same procedure. In general the probability of the first digit k can be expressed:
,
which goes together with the formula discovered by Newcomb and Benford.
Problem: Deduction according to Cohen (**)In the deduction of Benford`s Law according to Cohen about the scale invariance P(1)=log10(2) and P(2)=log10(3/2) were deduced by the scale invariance. Deduce analog to it the probability P(3) considering a multiplication of the set of values by factor 4!
Problem:
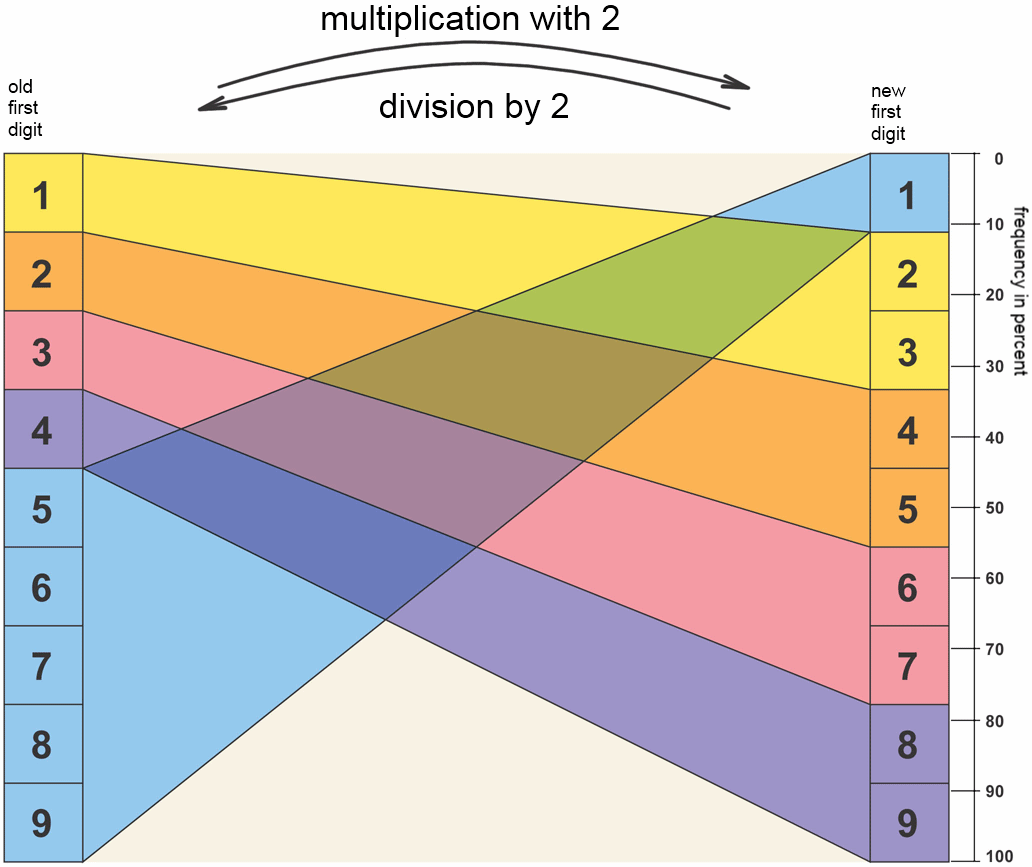
Illustration of scale invariance (**)Describe the figure concerning its significance in regard to scale invariance and Benford's Law!
[1]See Albrecht (2000), Page 35.
[2]See Pinkham (1961), Page 1223-1230.
[3]See Cohen (1976), Page 367-370.