 Benford's Law-
Historical Approach
Benford's Law-
Historical Approach Benford's Law-
Historical Approach
Benford's Law-
Historical ApproachStart | Overview of problems | Literatur | Credits
Worn logarithm tables (1881)
Benford`s diligent work (1938)
Scale invariance (1961)
Base invariance (1995)
Benford analysis (1998)
The history of Benford's-Lawbegins in the year 1881, as the american astronomer and mathematician Simon Newcomb discovered, that the first pages of logarithm tables in libraries were more worn out than the pages in the back. Such an observation would not be surprising if it were only about novelPage With such it would be common for people to pick a book, start reading, disliking it and putting it down again without finishing to read. Even with scientific books this would be possible, if the reader considers the book too easy or to challenging. It is absolutely reasonable for many people at the library to only read the first pages but not the rest of books like novels or science bookPage
But logarithm tables were only used in practical terms, to assist with calcu lations during those former days, which justifies Necombs astonishment. Logarithm tables are books, recording the logarithm of numbers in charts, using 10 as a basiPage Here we have to consider the logarithm of a number being made up by two parts: index - the integer part, and the Matisse [1] (the fractional part). Where as Mantissa defines the digital structure of a number, the index refers to the position of the comma more specifically the dimensions of the number.
For example the logarithms of 21 (log10(21)=1,322) and 2,1 (log10(2,1)=0,322) show the same mantissa but different indexes 21=2,1·101 and 2,1=2,1·100, because they only differ from each other by
the comma position.
The key is, to just document the mantissas in logarithm tables, meaning just the digits after the comma of the logarithm, so one decade put in a chart is enough (i.e. from 1000 to 9999). In logarithm tables the numbers with the first digit 1 are first, then 2 and so on. Because the dimensions of numbers are irrelevant, the order in logarithm tables is different from what we are familiar when counting, where numbers after a decimal power start all over with 1.
From his observation, that the first pages of logarithm tables are more worn than the last, Newcomb concluded, that numbers, starting with a low first digit are looked up more often, than numbers, starting with higher digitPage He concluded that there are more numbers starting with a low first digit than numbers with bigger first digits, which is based on not the numbers but the mantissas of the logarithms being uniformly distributed.[2]Newcomb released his new observation 1881 in a two page article in the "American Journal of Mathematics", without any further detailed explanations and without any empiric proof he already gave the (Benford)- probabilities for the first and second digit.
To perform appropriately during lessons, you as a math teacher do not just need to be able to do mental math, but to also have a deeper understanding of it. In one problem the logarithm of 9,8 and 9800 are to be calculated.
Newcombs discovery was hardly noticed and soon forgotten about.[3]More than half a century later the american physician Frank Benford came across the same lawfulness as Newcomb as he also wondered about the irregularly worn logarithm tablePage [4] As he reflected he came to the same conclusions for the probabilities as Newcomb.
Unlike Newcomb he explicitly gave the formulae for the calculation of the probabilitiePage On top of that he brought proof with 20,000 empiric facts out of 20 different contextPage Among others there were the statistics of the american baseball league, all numbers of an edition of "Reader`s Digest", the atomic weight of elements, and the house numbers of american scientistPage He found that the first digit 1 shows with a probability of 30,6%, whereas the 9 as first digit only has a probability of 4,7%. All the other empiric probabilities of the other first digits can be read off the second last row of the following chart, that outlines Benford`s studies:
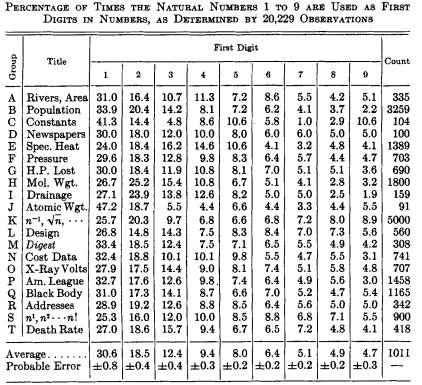
figure: Benford`s empirical study[5]
The empiric probabilities discovered by Benford were very surprising for many, because you could think that there would be no special reason to prefer a certain first digit, leaving us to think that it would be just as likely to have any first digit occur just like all otherPage Since there are 9 possible first digits the probability for each would be 1/9. This observation was clearly proven wrong by Benford`s empiric studiePage
Whereas the probabilities for the first and second digit given by Benford were easily proven, but appeared paradox to many, mathematicians, statisticians, physicians, economists, engineers and even amateurs[6]dealt with the so called "Benford Law"[7] and "The first digit law" and it`s lawfulnesPage
 Problem: Absolute, relative and cumulated frequentness (*)
Problem: Absolute, relative and cumulated frequentness (*)The figure above of Benford`s empirical studies is stated by relative frequenciePage Pick a row and give in addition to it the absolute frequency and the cumulated relative frequency. Mark down those three different interpretations against each other.
 Problem: Logarithm table (**)
Problem: Logarithm table (**)Comment on the following statement:
„If random numbers would be picked from 20.229 Benford`s data and
looked up on a nine pages logarithm table, the first page would be used six
times more, than the last page, in the long run."[8]
After Benford`s "first digit law" became more known, the question still stood, why this law would apply to so many different sources of data. Instead there were brought more empiric evidence of more sets of data abiding by Benford`s Law like the most common physical constants, the half life of spontaneous alpha decay, numbers on the front page of newspapers, stock prices and many otherPage On the other hand there were charts of numbers not abiding by Benford`s Law like: phone numbers of a certain region, charts with square roots, and generated random numberPage The question was how to classify the Benford Law by data which abide and those that do not.
Over a quater of a century scientists did not find the answers, considering the Benford Law a "whim of nature, beyond mathematical comprehension."[9]In the year 1961 a publication of the mathematician Rogers Pinkham of Rutgers University in New Brunswick made it more reputable. Pikham was able to proof the universal significance of Benford`s Law through a classical approach [10], claiming that the distribution of the first digit needs to be scale invariant. Pinkhams proofed the scale invariance of the probabilities of distribution given by Benford. On top of that he was able to give proof, that Benford`s Law is the only possible distribution fulfilling this condition. If there is a scale invariant distribution of the first digit, it needs to be a Benford distribution.[11]
Pinkhams publication significantly contributed to the credibility of Benford`s Law and was basis for many scientists to dig deeper into possible implications of Benford`s Law.
More recent publications are by Theordore P. Hill, a professor of mathematics at Georgia Institute of Technology, who was able to remove last doubts about Benford`s Law.
In 1995 he succeeded in a new approach of Benford`s Law by concluding
it only with the assumption of the base-invariance. [12]Base-invariance
means that Benford`s Law also applies not only to a decimal system, but
also remains valid to every other system of numbers with b as base. In addition to that Hill was able point out that base-invariance is already implied by scale-invariance, but not the other way around.t.
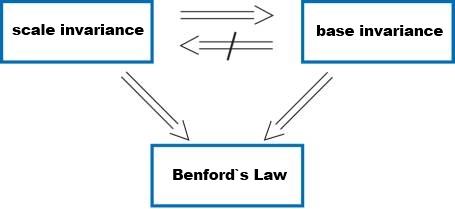
figure: scale invariance and base invariance[13]
After the acceptance of Benford`s Law in science, the question arouse, what use it is to know that the number of inhabitants of the 3141 regions in the US, the exchange rates at the New York stock market and the stocks traded there every day, just everything that can be counted, acts according to Benford`s Law. This problem was solved in 1995 by Mark Nigrini, who discovered the convenience to use the diversity of digits to test tax declarations and detect counterfeits, because the true ones should be following Benford`s Law.[14]Nigrini, who is now professor of accounting, thought it possible to use Benford`s law for examinations, because cheaters would just make up numbers, which do not apply Benford`s Law.
Nigrini developed a simple computer program, to examine big sets of numbers according to their Benford distribution. If the numbers of a companies accounting would differ significantly from the Benford distribution it would show possible counterfeit ambitionPage Some New York tax investigators tested the program on seven cases of cheating and it went off on all their cases, whereas Bill Clintons tax declaration for over 16 years did not show one wrong.[15]
Since 1998 Nigrinis "Detection Software" is used by the tax authorities of many american statePage The Benford-Analyse is also used in Germany by tax inspectors in the finance administration.[16]
[1]Mantissa, comes from latin, is a mathematical term to describe the decimal places after the comma of a logarithm. In informatics it also refers to the part of a float, that includes the digits and the algebraic sign of the number.
[2] See Newcomb (1881), Page 39-40.
[3] See Albrecht (2000), Page 35.
[4] See Benford (1938), Page 551.
[5] Source: Benford (1938), Page 553.
[6] See Raimi (1976), Page 521, Hill (1995a), Page 322 and Hill (1998), Page 359.
[7] To some degree the "first digits law" became wrongly known as Benford`s Law, because Newcomb described this law already in the year 1881. compare: Raimi (1976), Page 522 and Humenberger (2000), Page 139.
[8] See Raimi (1969b), Page 110.
[9] Albrecht (2000), Page 35.
[10] compare Posch (2004) p. 7. in the year 1969 Ralph Raimi from the university of Rochester was able to improve Pinkhams proof by taking a measure theoretical approach. To read more about that, look at: Raimi (1969a) p. 344, Humenberger (1996), p. 9 and Humenberger (2000) p. 146
[11] See Pinkham (1961), Page 1223-1230.
[12] See Hill (1995b), Page 887-895.
[13] Quelle: eigene Darstellung basierend auf Horn (1998), Page 25.
[14] See Nigrini (1999), Page 79-83.
[15] See Dworschak (1998), Page 228.
[16] See Blenkers, Becker (2005), Page 1 and Odenthal (2004), Page 1-2.