Benford's Law - Modern application

The American Karl Pearson developed the chi-square-test, a test from the area of statistics, used in various ways to help check if the observed frequency significantly differ from the frequentness that should apply because of theoretical conclusions or certain assumptions. It is also used in digital analysis of numbers and will be introduced here.[11]

While the Benford analysischecks on the distribution of the first digits, the inspector uses the Chi-square-test for the last pre-decimal position (or the last two pre-decimal positions or even the first decimal place),[12] where every one of the digits 0 to 9 occurs with the same frequentness of a 10%.
Because every person subconsciously has personal sympathies for or against certain numbers, you can count on systematic deviations if sets of numbers are manipulated or made up.[13]

In specific application of the chi-square-test a test statistic is assessed as:

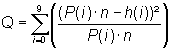
with h(i) as observed frequency of the pre-decimal position i and P(i)·n the theoretical expected frequency, which is the product of the theoretical frequency P(i) and the quantity n of the examined numbers. In this special case the probability P(i) is the same for all i - which is P(i)=0,1, so that all
test statistics Q are calculated with the following formula:

.

To differentiate, if the deviations of the frequency observed and the one expected are random or systematic, the value of the test statistic Q is compared to the quantile of the quantiles of the chi9-square-distribution, with 9 representing the quantity of degrees of freedom.[14]This procedure is based on the Theorem of Pearson which states that the equation of distribution

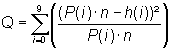
for n→∞onverges against the distribution function of a chi-square- distribution with k-1 degrees of freedom. As a rough guide you can say the
condition P(i)·n≥5 should be fulfilled for all i.[159]

Example:

If in our analysis of the test statistics Q of the last pre-decimal position shows anything higher than 19,02 or 21,67, it is 97,5% to 99% safe to speak of a systematical diversion. The probability of error of 2,5 % or 1% is called significance level. It states the probability of not-manipulated data to be presumed as systematically manipulated.

The other way around you can also state probabilities for predefined sets for the test statistics Q, according to the chi9-square-distribution, that abnormalities are of a random nature and without any special reason. The following chart shows, how it is already likely with a test statistics from 21 to 30 and even more so with a test statistics of 30, that the deviations in the analyzed set of data are not entirely coincidental.[16]

Q	P (deviation incidental)	P (special reason)
18	3,5 %	96,5 %
20	1,8 %	98,2 %
22	0,9 %	99,1 %
26	0,2 %	99,8 %
30	almost 0 %	almost 100 %

In one specific case irregularities in the accounting records of a freelancer were discovered with the help of the chi-square-test. It turned out that the man did not do his accounting accurately. It was found out that just before auditing, he had filled the spaces with devised numbers. The test also showed, that he preferred one particular number, without noticing it.[17]This example shows how the chi-square-test is a very effective means to detect made-up numbers in accounting. However it does not reveal and allow any conclusions about treacherous intentions. Those can only be answered by additional investigation.

Problem: Chi-square-test (**)

In an audit of a catering company the daily receipts of the years 1997 to 1999 were looked at. From among those 1,038 entries the analysis of the last pre-decimal digits showed probabilities of the following numbers as follows:

digit	0	1	2	3	4	5	6	7	8	9
rate / frequency	142	99	103	98	98	88	114	94	70	132

1. The chart above states the actual probabilities of each digit at the last pre-decimal place. Which probabilities might have been expected theoretically?
2. Decide with the help of the chi-square-test, if the diversions of the observed to the theoretically expected frequentness are of random nature or if they are already pointing towards a special cause! (Advice: Calculate the test statistic Q and compare it to the quantiles of the chi9-square-distribution!)
3. Make yourself familiar in the help menu of EXCEL with features like: CHITEST, CHIINV, CHIVERT and check within EXCEL with the help of this feature your result from point b), by calculating the test statistics Q and the probability for the diversions to be of random nature!

Prospect

At this point it is worth mentioning that digital analysis of numbers is a relatively young discipline, made possible by equipping audit test places with modern computers and software. In 2001 the guidelines about the Access to Data and the Check of Digital Documents (german: "Grundsätze zum Datenzugriff und zur Prüfung digitaler Unterlagen" GDPdU) were adjusted to modern ways of accounting in regard to the testing methods and techniques. Since 1^st of January 2002 it is possible to do a digital tax audit. Beginning of 2002 14,000 new IDEA test software licences were purchased by financial managements for this purpose.[18]It adds a new dimension to analysis with all their pros and cons. Relatively huge sets of data can quickly be evaluated on a large scale. Because the check is done completely, the frequency of testing is much higher and with that the likeliness to detect irregularities increases drastically.

There are only few practical experiences about digital tax audits made available at this point, but for the legal side it is ground breaking. The validity of these analysis programs of the finance authorities will definitely engage lawyers and courts.[19]At the same time we can expect an increase of digital audits and a transfer of analysis procedures from the area of digital analysis of numbers into other areas too.[20]

 

(back to start of page)

---

[1] See Browne (1998), Walthoe, Hunt, Pearson (1999) and Nigrini (1999), Page 79-83.

[2]See Matthews (2000), Page 30

[3] See Odenthal (2004), Page 1.

[4] See Hagenkötter, Mülot (2002), Page 55.

[5] Audicon GmbH, Stuttgart, Düsseldorf (www.audicon.net)

[6] See Blenkers, Becker (2005), Page 1.

[7] See Blenkers, Becker (2005), Page 4.

[8] See Odenthal (2004), Page 5-14.

[9] See Posch (2004), Page 13-15.

[10] See Odenthal (2004), Page 3

[11]The chi-square-test is according to the Hesse math curriculum (G8) scheduled to be part of the theme "Practical Stochastics" during the 12G.2 semester. (During the semester 12G.2 one of the following themes has to be chosen: ordinary differential equation, power series, numeric approximation procedures, approximation of equations, circle and cone, conic sections, practical stochastics, determinants and matrices, affine figures or mathematical structures and process of evidence.)

[12] or also the last two pre-decimal places or the first decimal place

[13] See Blenkers, Becker (2005), Page 2.

[14]The codomain of the feature is divided into 10 classes (digits 0 through 9). That is why there are 9 degrees of freedom, because the probability of the last class is defined by the nine other probabilities, because their sum has to be 100%.

[15] See Mosler, Schmid (2003), Page 273.

[16] See Blenkers (2004), Page 80.

[17] See o. V. (2006a).

[18] See Blenkers (2004), Page 130.

[18] See Hagenkötter, Mülot (2002), Page 26.

[18] See Blenkers (2004), Page 77 and Blenkers, Becker (2005), Page 10.