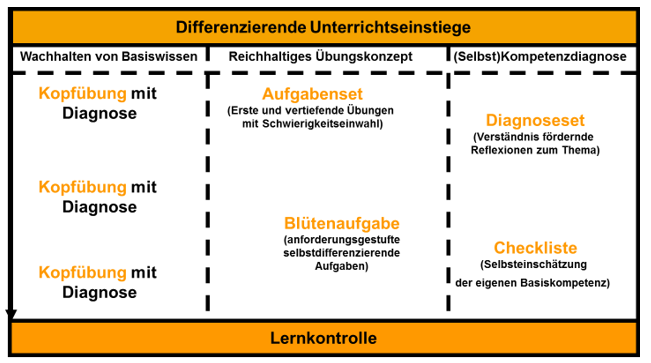
Gemeinsam mit Projektlehrkräften von MABIKOM wurden die vier fachdidaktischen Kernelemente mit Methodenbausteinen verknüpft und „typische“ Methodenbausteine erarbeitet. Für die Umsetzung dieser Kernelemente können unterschiedliche Methoden und Organisationsformen in Frage kommen, sodass die Umsetzung variieren kann.
Die entwickelten Methodenbausteine sind in der folgenden Abbildung dargestellt und werden in diesem Abschnitt noch weiter erläutert.

Klicken Sie auf die folgenden Überschriften, um den entsprechenden Methodensteckbrief herunterzuladen. Am Ende jedes Methodenabschnittes finden Sie ausklappbare Beispiele für eine Umsetzung der Methoden.
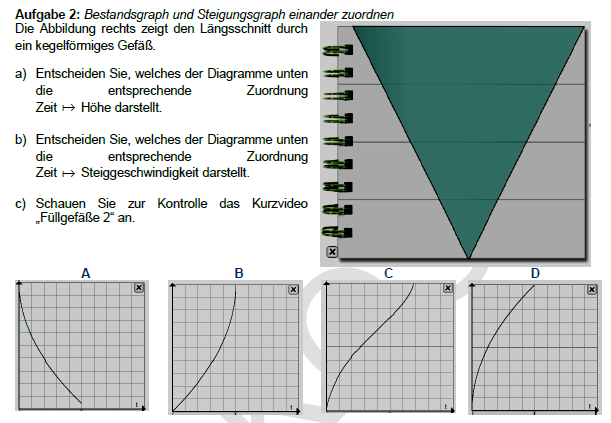
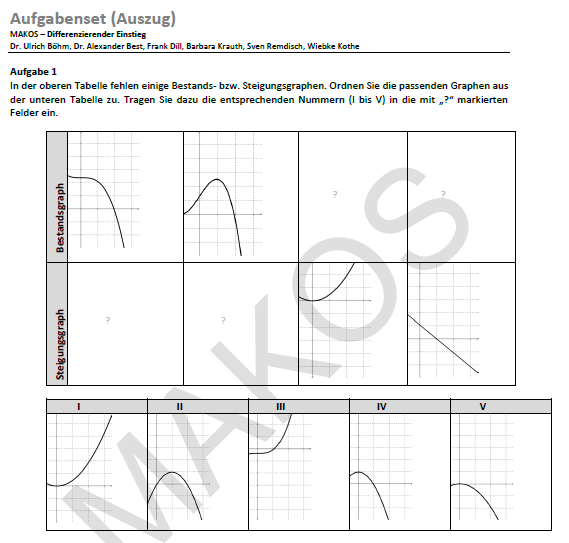
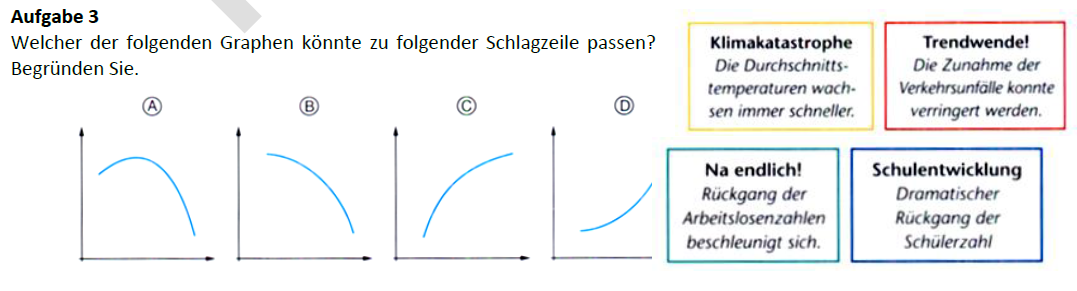
1. Differenzierende und weittragende Unterrichtseinstiege
Differenzierende Unterrichtseinstiege schaffen unterschiedliche Zugänge zu einem Thema. Darüber hinaus werden, im Gegensatz zu konventionellen kleinschrittigen Einstiegen, bereits in der ersten Stunde zentrale Aspekte des neuen Themas angesprochen. So wird es den Schüler_innen erleichtert individuelle Lernziele auszubilden. Sie können schon früh eine Grundvorstellung der neuen Lerninhalte bilden und diese für den anschließenden Lernprozess nutzen.
Die Differenzierung bei Einstiegen wird über Wahlmöglichkeiten verschiedener Anwendungen umgesetzt. Dabei kann der differenzierende Ansatz bezüglich der Kontexte, Darstellungsformen und Erkenntnisebenen realisiert werden, wobei ebenfalls verschiedene Lernstile berücksichtigt werden sollten. Dabei könnte die methodische Umsetzung mittels eines Gruppenpuzzels oder Stationenlernen erfolgen. In einer anschließenden Ergebnissicherung werden gemeinsame mathematische Strukturen herausgearbeitet und die Aufgaben miteinander in Verbindung gebracht.
Mit der Entwicklung von Handreichungen differenzierender Einstiege im MAKOS Projekt werden zum einen Lerhrer_innen verschiedene Einstiegsmöglichkeiten aufgezeigt. Zum anderen werden bei der Umsetzung vergleichsweise mehr Schüler_innen motiviert und die Ausbildung von eigenständigen Lernzielen wird unterstützt, da die Schüler_innen Aufgaben nach ihren individuellen Interessen oder Können auswählen.
2. Kopfübungen
Um die gesteckten Lernziele realisieren zu können, ist immer ein gewisses Grundwissen und Grundkönnen zu grundlegenden mathematischen Inhalten notwendig. Dieses ist jedoch bei Schüler_innen oft sehr unterschiedlich ausgeprägt.
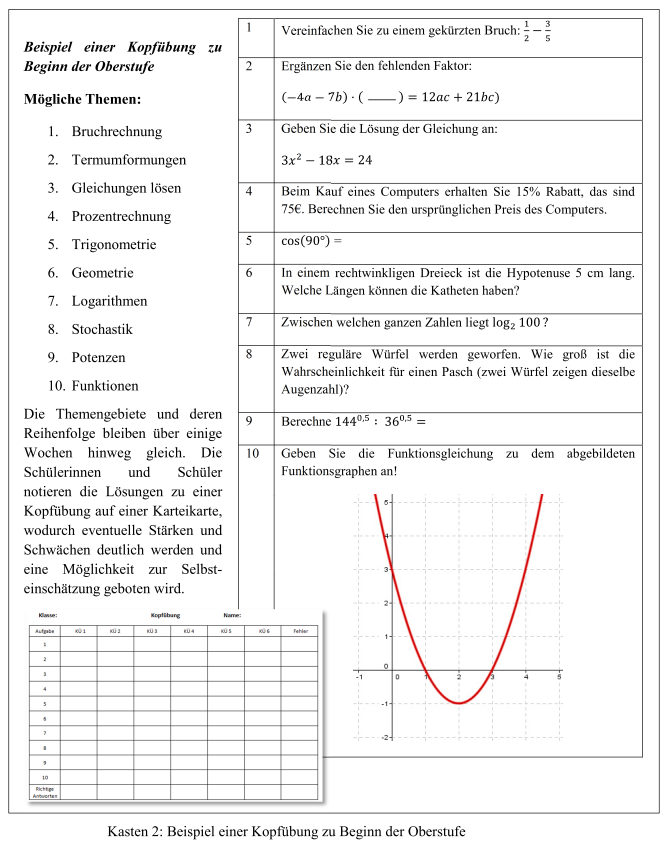
Deshalb wird versucht dieses Grundwissen und -können durch die Methode der „vermischten Kopfübungen“ wachzuhalten. Darüber hinaus können individuelle Wissenslücken diagnostiziert und anschließend selbstständig geschlossen werden.
Die vermischt Kopfübung sollte im Unterrichtsalltag zu einem wöchentlichen Ritual werden und inklusive Auswertung ca. 10-15 Minuten Zeit beanspruchen. Die vermischte Kopfübung umfasst maximal 10 Aufgaben und wird im Kopf gelöst. Dabei gehen die Aufgabe über formale Operationen hinaus und prüfen das Verständnis grundlegender Begriffe, Sätze und Verfahren. Die Aufgaben bleiben einige Wochen thematisch in der selben Reihenfolge, sodass den Schüler_innen eine Selbstdiagnose ermöglicht wird.
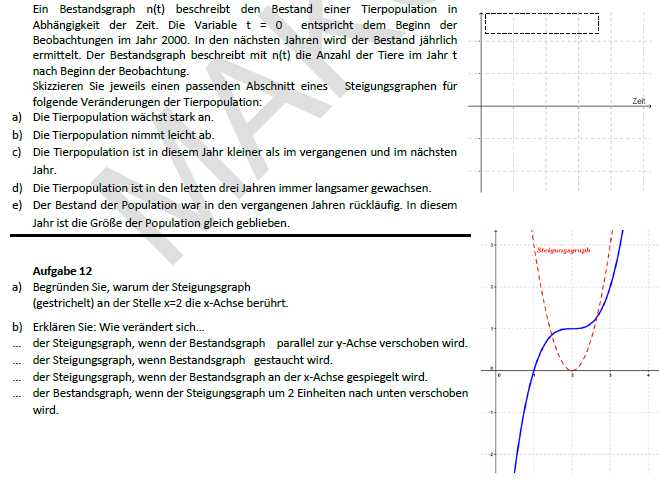
3. Aufgabenset mit Selbsteinschätzungsbogen
Im Aufgabenset wird die Differenzierung über Wahlmöglichkeiten realisiert. Dabei wird der Vorstellung „Alle üben alles“ den Rücken gekehrt. Beim Aufgabenset handelt es sich um ein schwierigkeitsgestuftes Aufgabenangebot, welches in einer vorgegebenen Zeit bearbeitet wird. Dabei wird von den Schüler_innen eine Mindestanzahl an Aufgaben zur Bearbeitung gefordert. Das Aufgabenset eignet sich bereits zur ersten Übung eines neuen Themas und beinhaltet eine niedrigschwellige Einstiegsaufgabe. Leistungsstarke Schüler_innen können niedrigschwellige Einstiege überspringen und mit vertiefenden Aufgaben beginnen. Damit erfolgt die Differenzierung über das Level der Einstiegsaufgabe, sowie die Anzahl der bearbeiteten Aufgaben.
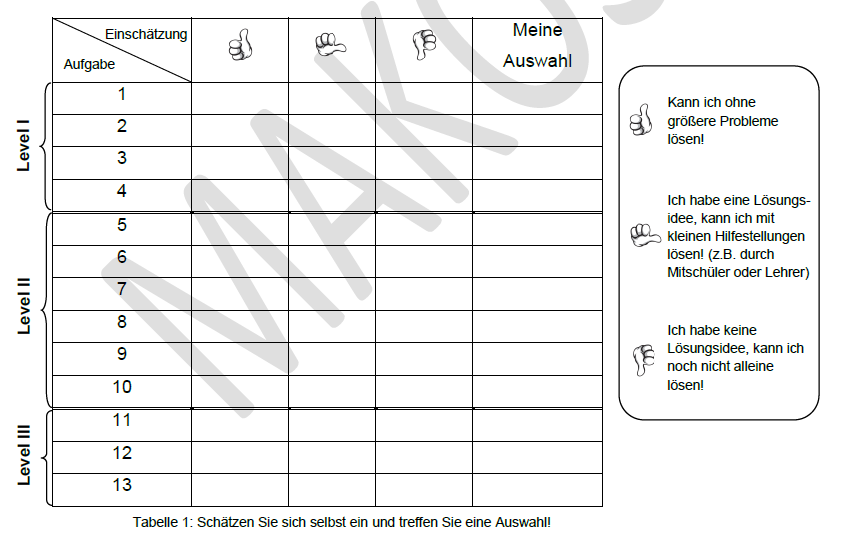
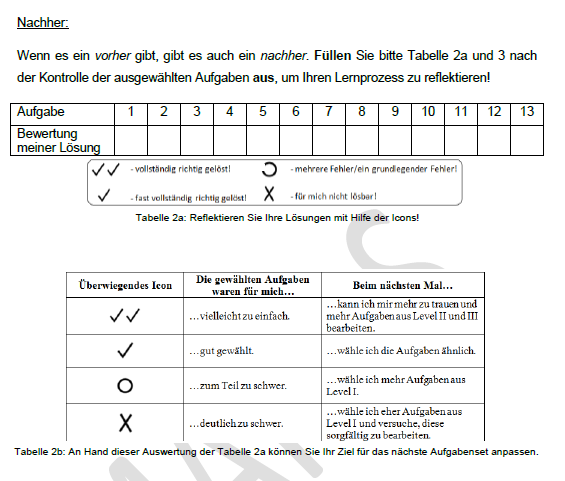
Mit dem Selbsteinschätzungsbogen sollen die Schüler_innen bei der Bearbeitung des Aufgabensets unterstützt werden. Sie werden in der Auswahl der Aufgaben unterstützt und es wird gleichzeitig eine realistische Selbsteinschätzung gefördert. Die Schüler_innen werden dazu aufgefordert zunächst alle Aufgaben zu lesen und einzuschätzen, ob sie die Aufgaben lösen können. Anschließend werden die Schüler_innen dazu aufgefordert ihre Arbeit zu bewerten und daraus einen Schluss für das nächste Arbeiten mit Wahlaufgaben zu ziehen. Zuletzt wird das mathematische Können eingeschätzt und Hinweise zum weiterarbeiten gegeben.
4. Blütenaufgabe
Blütenaufgaben sind ebenfalls eine Form des differenzierten Übungskonzepts. Dabei handelt es sich um eine besondere Form des Arbeitens mit Wahlaufgaben. Bei einer Blütenaufgabe werden zu einem inner- oder außermathematischen Kontext drei bis fünf Teilaufgaben gestellt und ermöglicht die Bearbeitung eines mathematischen Kontexts auf unterschiedlichen Niveau. Der Einstieg erfolgt zunächst niederschwellig, die mittleren Aufgaben umfassen den Regelstandard und die letzten Aufgaben umfassen den Optimalstandard. Dabei werden die Teilaufgaben immer offener gestaltet, wobei dies nicht zwingend notwendig ist.
Die Schüler_innen erhalten den Arbeitsauftrag entweder eine bestimmte Anzahl Aufgaben zu bearbeiten oder in einer vorgegebenen Zeit so weit wie möglich zu kommen.
5. Diagnoseset
Um effektiv mit differenzierenden Angeboten zu arbeiten, ist eine realistische Selbsteinschätzung zwingend notwendig. Daher werden die Schüler_innen durch das Diagnoseset und die Checkliste in ihrer Selbsteinschätzung gefördert. Durch das Diagnoseset haben die Schüler_innen die Möglichkeit schon kurz nach dem Themeneinstieg ein systematisches Feedback zu bekommen.
Das Diagnoseset wird nach der Einführungsstunde und ersten Übung eingesetzt und ist ein unbenoteter Kurztest. Er thematisiert die zentralen Aspekte des neuen Themeninhalts und diagnostiziert und fördert ein Grundverständnis zu dem neuen Thema. Durch die folgende Aufgabenformate eines Diagnosesets wird eine verständnisfördernde Reflexion erreicht.
- Erläutern des Einstiegsbeispiels (Worum geht es?)
- Lösen einer Grundaufgabe und ihrer Umkehrung.
- Herstellen von Sinn- und Sachbezug (Wo kann man das Neue anwenden und wo nicht?). (Beurteilen von Aussagen/Zuordenen von Grafiken (wahr oder falsch)/Finden von Fehlern)
- Benennen typischer Fehler.
Für die Bearbeitung stehen den Schüler_innen etwa 15 Minuten zur Verfügung, sie erfolgt in schriftlicher Einzelarbeit und die Auswertung erfolgt selbstständig. Das Diagnoseset bietet die Gelegenheit für eine frühzeitige Diagnose des Lernstandes und gibt dadurch eine Orientierungshilfe für wichtige Inhalte sowie den eigenen Lernprozess.
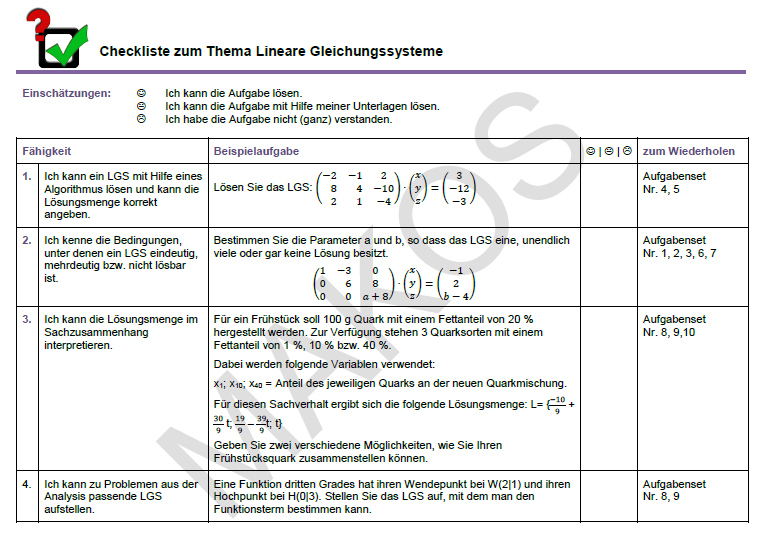
6. Checkliste
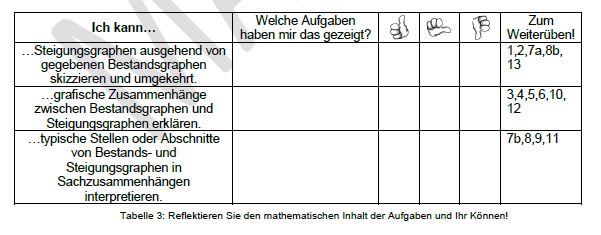
Die Checkliste ist eine Hilfestellung zur Selbsteinschätzung vor einer Leistungsprüfung. Sie enthält die grundlegenden Wissens- und Könnenselemente eines Themas. Durch die Verwendung von „Ich kann…“-Formulierungen und der Illustrierung durch Beispielaufgaben, wird den Schüler_innen die Möglichkeit gegeben den individuellen Lernstand einzuschätzen. Darüberhinaus werden Verweise zu weiteren Übungen gegeben, sodass an individuellen Schwächen gearbeitet werden kann.